Common Lisp the Language, 2nd Edition




Next: Implementation Parameters
Up: Numbers
Previous: Byte Manipulation Functions
The
Common Lisp facility for generating pseudo-random numbers has
been carefully defined to make its use reasonably portable.
While two implementations may produce different series
of pseudo-random numbers, the distribution of values should
be relatively independent of such machine-dependent aspects
as word size.
[Function]
random number &optional state
(random n) accepts a positive number n and returns
a number of the same kind between zero (inclusive) and n (exclusive).
The number n may be an integer or a floating-point number.
An approximately uniform choice distribution is used.
If n is an integer, each of the possible results
occurs with (approximate) probability
1/n.
(The qualifier ``approximate'' is used because of implementation
considerations; in practice, the deviation from uniformity should be
quite small.)
The argument state must be an object of type random-state;
it defaults to the value of the variable *random-state*.
This object is used to maintain the state of the pseudo-random-number
generator and is altered as a side effect of the random operation.
Compatibility note: random of zero arguments as defined in MacLisp
has been omitted because
its value is too implementation-dependent (limited by fixnum range).
Implementation note: In general, even if random of zero arguments
were defined as in MacLisp,
it is not adequate to define (random n) for integral n
to be simply (mod (random) n); this fails to be uniformly distributed
if n is larger than the largest number produced by random,
or even if n merely approaches this number.
This is another reason for omitting random of zero arguments in Common Lisp.
Assuming that the underlying mechanism produces ``random bits''
(possibly in chunks such as fixnums), the best approach is to produce
enough random bits to construct an integer k some number d of bits
larger than (integer-length n) (see integer-length), and
then compute (mod k n). The quantity d should be at
least 7, and preferably 10 or more.
To produce random floating-point numbers in the half-open
range [A, B),
accepted practice (as determined by a look through the
Collected Algorithms from the ACM, particularly algorithms
133, 266, 294, and 370) is to compute
X * (B - A) + A,
where X is a floating-point number uniformly distributed over
[0.0, 1.0)
and computed by calculating a random integer N in the range
[0, M)
(typically by a multiplicative-congruential or linear-congruential method
mod M) and then setting X = N/M. See also [27].
If one takes 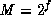 , where f is the length of the significand
of a floating-point number (and it is in fact common to choose M
to be a power of 2), then this method is equivalent to the following
assembly-language-level procedure. Assume the representation
has no hidden bit. Take a floating-point 0.5,
and clobber its entire significand with random bits. Normalize the
result if necessary.
, where f is the length of the significand
of a floating-point number (and it is in fact common to choose M
to be a power of 2), then this method is equivalent to the following
assembly-language-level procedure. Assume the representation
has no hidden bit. Take a floating-point 0.5,
and clobber its entire significand with random bits. Normalize the
result if necessary.
For example, on the DEC PDP-10, assume that accumulator T is completely random
(all 36 bits are random). Then the code sequence
LSH T,-9 ;Clear high 9 bits; low 27 are random
FSC T,128. ;Install exponent and normalize
will produce in T a random floating-point number uniformly distributed
over [0.0, 1.0). (Instead of the LSH instruction,
one could do
TLZ T,777000 ;That's 777000 octal
but if the 36 random bits came from a congruential random-number generator,
the high-order bits tend to be ``more random'' than the low-order ones,
and so the LSH would be better for uniform distribution.
Ideally all the bits would be the result of high-quality randomness.)
With a hidden-bit representation, normalization is not a problem,
but dealing with the hidden bit is. The method can be adapted as follows.
Take a floating-point 1.0 and clobber the explicit significand bits with
random bits; this produces a random floating-point number in
the range [1.0, 2.0). Then simply subtract 1.0. In effect, we
let the hidden bit creep in and then subtract it away again.
For example, on the DEC VAX, assume that register T is
completely random (but a little less random than on the PDP-10, as
it has only 32 random bits). Then the code sequence
INSV #^X81,#7,#9,T ;Install correct sign bit and exponent
SUBF #^F1.0,T ;Subtract 1.0
will produce in T a random floating-point number uniformly distributed
over [0.0, 1.0). Again, if the low-order bits are not random enough,
then the instruction
ROTL #7,T
should be performed first.
Implementors may wish to consult reference [41] for
a discussion of some efficient methods of generating pseudo-random numbers.
[Variable]
*random-state*
This variable holds a data structure,
an object of type random-state, that encodes the internal state
of the random-number generator that random uses by default.
The nature
of this data structure is implementation-dependent. It may be
printed out and successfully read back in, but may or may not function
correctly as a random-number state object in another implementation.
A call to random will perform a side effect on this data structure.
Lambda-binding this variable to a different random-number state object
will correctly save and restore the old state object.
[Function]
make-random-state &optional state
This function returns a new object of type random-state,
suitable for use as the value of the variable *random-state*.
If state is nil or omitted, make-random-state returns a copy
of the current random-number state object (the value of
the variable *random-state*). If state is a state object,
a copy of that state object is returned. If state is t,
then a new state object is returned that has been ``randomly''
initialized by some means (such as by a time-of-day clock).
Rationale: Common Lisp purposely provides no way to initialize a random-state
object from a user-specified ``seed.'' The reason for this is that
the number of bits of state information in a random-state object
may vary widely from one implementation to another, and there is no
simple way to guarantee that any user-specified seed value will be
``random enough.'' Instead, the initialization of random-state
objects is left to the implementor in the case where the argument t
is given to make-random-state.
To handle the common situation of executing the same program many times
in a reproducible manner, where that program uses random, the following
procedure may be used:
-
Evaluate (make-random-state t) to create a random-state object.
-
Write that object to a file, using print, for later use.
-
Whenever the program is to be run, first use read to create
a copy of the random-state object from the printed representation
in the file.
Then use the random-state object newly created by the read operation
to initialize the random-number generator for the program.
It is for the sake of this procedure for reproducible execution that
implementations are required to provide a read/print syntax for objects
of type random-state.
It is also possible to make copies of a random-state object
directly without going through the print/read process, simply by
using the make-random-state function to copy the object; this allows
the same sequence of random numbers to be generated many times
within a single program.
Implementation note: A recommended way to implement the type random-state
is effectively to use the machinery for defstruct.
The usual structure syntax may then be used for printing random-state
objects; one might look something like
#S(RANDOM-STATE DATA #(14 49 98436589 786345 8734658324 ...))
where the components are of course completely implementation-dependent.
[Function]
random-state-p object
random-state-p is true if its argument is a random-state object,
and otherwise is false.
(random-state-p x) == (typep x 'random-state)




Next: Implementation Parameters
Up: Numbers
Previous: Byte Manipulation Functions
AI.Repository@cs.cmu.edu
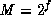 , where f is the length of the significand
of a floating-point number (and it is in fact common to choose M
to be a power of 2), then this method is equivalent to the following
assembly-language-level procedure. Assume the representation
has no hidden bit. Take a floating-point 0.5,
and clobber its entire significand with random bits. Normalize the
result if necessary.
, where f is the length of the significand
of a floating-point number (and it is in fact common to choose M
to be a power of 2), then this method is equivalent to the following
assembly-language-level procedure. Assume the representation
has no hidden bit. Take a floating-point 0.5,
and clobber its entire significand with random bits. Normalize the
result if necessary.